Understand AVL Trees
Table of contents:
What is an AVL Tree?
An AVL Tree (named after inventors Adelson-Velsky and Landis) is a self-balancing Binary Search Tree (BST) widely used in databases to ensure efficient data retrieval and updates. By maintaining a balance factor (the height difference between left and right subtrees) of at most 1 for every node, AVL Trees keep operations like search, insertion, and deletion efficient at O(log n). This makes them ideal for indexing and query optimization, where maintaining balanced structures ensures consistently fast performance.
Understand AVL Trees
AVL Trees are one of the most important data structures in computer science. They maintain balance in binary search trees (BSTs) to ensure efficient operations. This guide covers AVL Trees comprehensively, including insertion, balancing, rotations, deletion, and traversals, while incorporating examples from the DB.c project. Check out the full codebase on my GitHub repository .
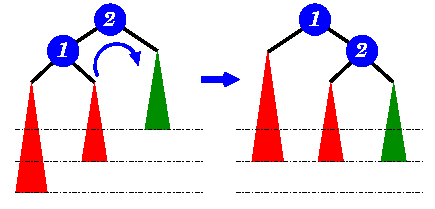
Real-World Analogy
Think of a bookshelf where books are organized by height. If one side grows taller than the other, it becomes difficult to access books efficiently. AVL Trees act like a librarian, constantly rearranging the books to keep the balance intact.
Structure
Each node in an AVL Tree contains:
- A value
- References to its left and right children
- A height attribute to calculate balance factors
Here’s the node structure:
typedef struct AVL_NODE
{
int value;
int height;
struct AVL_NODE *left;
struct AVL_NODE *right;
} AVL_NODE;
AVL_NODE *avl_create_node(int value)
{
AVL_NODE *node = (AVL_NODE *)malloc(sizeof(AVL_NODE));
node->value = value;
node->height = 1;
node->left = node->right = NULL;
return node;
}
Balance
In AVL Trees, balance is a measure of how evenly distributed the heights of the left and right subtrees are for any given node. The balance factor is calculated as:
Balance Factor = Height of Left Subtree - Height of Right Subtree
Balance Factor
- Balance Factor = 0: Both left and right subtrees have the same height, indicating perfect balance.
- Balance Factor = 1: The left subtree is taller by one level.
- Balance Factor = -1: The right subtree is taller by one level.
- Balance Factor > 1 or < -1: The node is unbalanced, and rotations are required to restore balance.
Example: Balance Calculation
Tree:
20
/ \
10 30
/
25
-
For Node 20:
- Height of Left Subtree = 1 (Node 10)
- Height of Right Subtree = 2 (Nodes 30 → 25)
- Balance Factor = 1 - 2 = -1 (Balanced)
-
For Node 30:
- Height of Left Subtree = 1 (Node 25)
- Height of Right Subtree = 0
- Balance Factor = 1 - 0 = 1 (Balanced)
-
For Node 10 and Node 25:
- Both have no children, so their balance factors are 0 (Perfectly balanced).
Unbalanced Cases:
1. Left-Heavy Imbalance (Balance Factor > 1):
30
/
20
/
10
- For Node 30:
- Height of Left Subtree = 2 (Nodes 20 → 10)
- Height of Right Subtree = 0
- Balance Factor = 2 - 0 = 2 (Unbalanced)
2. Right-Heavy Imbalance (Balance Factor < -1):
10
\
20
\
30
- For Node 10:
- Height of Left Subtree = 0
- Height of Right Subtree = 2 (Nodes 20 → 30)
- Balance Factor = 0 - 2 = -2 (Unbalanced)
3. Left-Right Imbalance (Balance Factor > 1 in Left Subtree with Right-Heavy Subtree):
30
/
10
\
20
- For Node 30:
- Height of Left Subtree = 2 (Nodes 10 → 20)
- Height of Right Subtree = 0
- Balance Factor = 2 - 0 = 2 (Unbalanced)
- For Node 10:
- Height of Left Subtree = 0
- Height of Right Subtree = 1 (Node 20)
- Balance Factor = 0 - 1 = -1 (Unbalanced Subtree)
4. Right-Left Imbalance (Balance Factor < -1 in Right Subtree with Left-Heavy Subtree):
10
\
30
/
20
- For Node 10:
- Height of Left Subtree = 0
- Height of Right Subtree = 2 (Nodes 30 → 20)
- Balance Factor = 0 - 2 = -2 (Unbalanced)
- For Node 30:
- Height of Left Subtree = 1 (Node 20)
- Height of Right Subtree = 0
- Balance Factor = 1 - 0 = 1 (Unbalanced Subtree)
Importance of Balance
Maintaining balance ensures that AVL Tree operations like search, insertion, and deletion always have O(log n) complexity. An unbalanced tree degrades into a linear structure, resembling a linked list, where operations take O(n).
By automatically adjusting the balance factor and applying rotations during insertions and deletions, AVL Trees remain efficient and reliable for various applications.
Insertion
Insertion in AVL Trees automatically ensures balance by performing rotations when required. Here’s the insertion function:
AVL_NODE *avl_insert_node(AVL_NODE *root, int value)
{
if (root == NULL)
return avl_create_node(value);
if (value < root->value)
root->left = avl_insert_node(root->left, value);
else if (value > root->value)
root->right = avl_insert_node(root->right, value);
avl_update_height(&root);
int balance = avl_get_balance(root);
// Perform rotations based on balance factor
// Case 1: Left-Left (LL)
if (balance > 1 && value < root->left->value)
return avl_rotation_right(root);
// Case 2: Right-Right (RR)
if (balance < -1 && value > root->right->value)
return avl_rotation_left(root);
// Case 3: Left-Right (LR)
if (balance > 1 && value > root->left->value)
{
root->left = avl_rotation_left(root->left);
return avl_rotation_right(root);
}
// Case 4: Right-Left (RL)
if (balance < -1 && value < root->right->value)
{
root->right = avl_rotation_right(root->right);
return avl_rotation_left(root);
}
return root;
}
Rotation Conditions
- Left-Left (LL): When a node is inserted into the left subtree of a left child, causing imbalance. Solution: Perform a single right rotation.
Before Rotation: After Rotation:
30 20
/ / \
20 ---> 10 30
/
10
- Right-Right (RR): When a node is inserted into the right subtree of a right child, causing imbalance. Solution: Perform a single left rotation.
Before Rotation: After Rotation:
10 20
\ / \
20 ---> 10 30
\
30
- Left-Right (LR): When a node is inserted into the right subtree of a left child. Solution: Perform a left rotation on the left child, followed by a right rotation on the root.
Before Rotations: After Left: After Right:
30 30 20
/ / / \
10 ---> 20 ---> 10 30
\ /
20 10
- Right-Left (RL): When a node is inserted into the left subtree of a right child. Solution: Perform a right rotation on the right child, followed by a left rotation on the root.
Before Rotations: After Right: After Left:
10 10 20
\ \ / \
30 ---> 20 ---> 10 30
/ \
20 30
- Left-Left (LL): When a node is inserted into the left subtree of a left child, causing imbalance. Solution: Perform a single right rotation.
- Right-Right (RR): When a node is inserted into the right subtree of a right child, causing imbalance. Solution: Perform a single left rotation.
- Left-Right (LR): When a node is inserted into the right subtree of a left child. Solution: Perform a left rotation on the left child, followed by a right rotation on the root.
- Right-Left (RL): When a node is inserted into the left subtree of a right child. Solution: Perform a right rotation on the right child, followed by a left rotation on the root.
Example: Insertions and Rotations
Insert 10 + 20
10
\
20
Insert 30 (Triggers RR Rotation)
Before Rotation: After Rotation:
10 20
\ / \
20 ---> 10 30
\
30
Insert 25 (Triggers RL Rotation)
Before Rotations: After Right: After Left:
10 10 20
\ \ / \
30 ---> 25 ---> 10 30
/ \
25 30
Rotations in Detail
Deletion in AVL Trees
Deletion in AVL Trees involves removing a node and ensuring the tree remains balanced by performing rotations if needed. Here’s how deletion works:
Steps of Deletion
- Find the Node to Delete: Traverse the tree to locate the node.
- Delete the Node: If the node has:
- No children: Simply remove it.
- One child: Replace the node with its child.
- Two children: Replace the node with its in-order successor (smallest node in the right subtree).
- Update Heights: After deletion, update the heights of the nodes.
- Rebalance: Check the balance factor and perform rotations if needed.
Example: Deletion Function
AVL_NODE *avl_delete_node(AVL_NODE *root, AVL_NODE *target)
{
if (root == NULL)
{
return root;
}
// Start with BST delete logic
if (root->value > target->value)
{
root->left = avl_delete_node(root->left, target);
}
else if (root->value < target->value)
{
root->right = avl_delete_node(root->right, target);
}
else
{
// Case 1: no child
if (root->right == NULL && root->left == NULL)
{
free(root);
return NULL;
}
// Case 2: one child
else if (root->right == NULL || root->left == NULL)
{
AVL_NODE *tmp = (root->right) ? (root->right) : (root->left);
free(root);
root = tmp;
}
// Case 3: both children
else
{
AVL_NODE *proc = NULL;
AVL_NODE *suc = NULL;
avl_find_predecessor_successor(root, target->value, &proc, &suc);
root->value = suc->value;
root->right = avl_delete_node(root->right, suc);
}
}
if (root == NULL)
return root;
// Update height of the current node
avl_update_height(&root);
// Get balance factor
int balance = avl_get_balance(root);
// Left Left Case
if (balance > 1 && avl_get_balance(root->left) >= 0)
return avl_rotation_right(root);
// Left Right Case
if (balance > 1 && avl_get_balance(root->left) < 0)
{
root->left = avl_rotation_left(root->left);
return avl_rotation_right(root);
}
// Right Right Case
if (balance < -1 && avl_get_balance(root->right) <= 0)
return avl_rotation_left(root);
// Right Left Case
if (balance < -1 && avl_get_balance(root->right) > 0)
{
root->right = avl_rotation_right(root->right);
return avl_rotation_left(root);
}
return root;
}
Example: Delete 20
Tree before deletion:
20
/ \
10 30
After deletion:
30
/
10
Balancing operations restore the AVL property if violated.
1. Right Rotation (LL Case)
Occurs when a left-heavy imbalance arises:
Before Rotation: After Rotation:
30 20
/ / \
20 ---> 10 30
/
10
AVL_NODE *avl_rotation_right(AVL_NODE *y)
{
AVL_NODE *x = y->left;
AVL_NODE *z = x->right;
x->right = y;
y->left = z;
avl_update_height(&y);
avl_update_height(&x);
return x;
}
2. Left Rotation (RR Case)
Occurs when a right-heavy imbalance arises:
Before Rotation: After Rotation:
10 20
\ / \
20 ---> 10 30
\
30
AVL_NODE *avl_rotation_left(AVL_NODE *x)
{
AVL_NODE *y = x->right;
AVL_NODE *z = y->left;
y->left = x;
x->right = z;
avl_update_height(&x);
avl_update_height(&y);
return y;
}
3. Left-Right Rotation (LR Case)
Occurs when a node is inserted into the right subtree of a left child:
Before Rotations: After Left: After Right:
30 30 20
/ / / \
10 ---> 20 ---> 10 30
\ /
20 10
4. Right-Left Rotation (RL Case)
Occurs when a node is inserted into the left subtree of a right child:
Before Rotations: After Right: After Left:
10 10 20
\ \ / \
30 ---> 20 ---> 10 30
/ \
20 30
Traversals
In-Order Traversal
An in-order traversal visits nodes in ascending order of their values: left subtree, root, right subtree. This traversal is especially useful for printing tree elements in sorted order.
void avl_inorder_traverse(AVL_NODE *node, void(callback)(AVL_NODE *node))
{
if (node == NULL)
return;
avl_inorder_traverse(node->left, callback);
callback(node);
avl_inorder_traverse(node->right, callback);
}
Example:
void print_node_value(AVL_NODE *node)
{
printf("%d ", node->value);
}
avl_inorder_traverse(root, print_node_value);
Tree:
20
/ \
10 30
Output:
10 20 30
Level-Order Traversal
A level-order traversal (or breadth-first traversal) visits nodes level by level, starting from the root. This traversal is useful for visualizing the tree structure.
void avl_lvlorder_traverse(AVL_NODE *node, void(callback)(AVL_NODE *node))
{
if (node == NULL) return;
Queue *q = create_queue();
enqueue(q, node);
while (!queue_is_empty(q))
{
AVL_NODE *current = dequeue(q);
callback(current);
if (current->left != NULL)
enqueue(q, current->left);
if (current->right != NULL)
enqueue(q, current->right);
}
free(q);
}
Example:
avl_lvlorder_traverse(root, print_node_value);
Tree:
20
/ \
10 30
Output:
20 10 30
Conclusion
AVL Trees are a foundational data structure for balanced and efficient operations. This guide covers all aspects, from insertion to traversals. For further implementation details and complete source code, explore the DB.c project on GitHub .